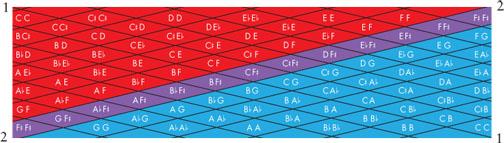
A few years ago, Princeton University music theorist and composer Dmitri Tymoczko was sitting in the living room of his home playing with a piece of paper. Printed on the sheet were rows and columns of dots representing all the two-note chords that can be played on a piano — AA, AB b , AB, and so on for the rows; AA, B b A, BA, and so on for the columns. It was a simple drawing, something a child could make, yet Tymoczko felt that the piece of paper was trying to show him something that no one ever had seen before.
Suddenly Tymoczko (pronounced tim-OSS-ko) realized that if he cut two triangles from the piece of paper, turned one of the triangles upside down, and reconnected the two triangles where the chords overlapped, the two-note chords on one edge of the resulting strip of paper would be the reversed versions of those on the opposite edge. If he then twisted the paper and attached the two edges, the chords would line up. “That’s when I got a tingly feeling in my fingers,” he says.
Tymoczko had discovered the fundamental geometric shape of two-note chords. They occupy the space of a Möbius strip, a two-dimensional surface embedded in a three-dimensional space. Music is not just something that can be heard, he realized. It has a shape.
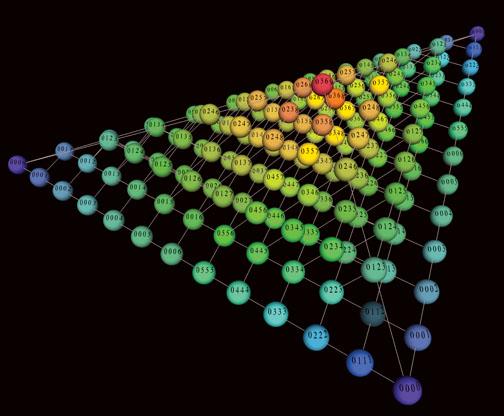
He soon saw that he could transform more complex chords the same way. Three-note chords occupy a twisted three-dimensional space, and four-note chords live in a corresponding but impossible-to-visualize four-dimensional space. In fact, it worked for any number of notes — each chord inhabit ed a multidimensional space that twisted back on itself in unusual ways — a non-Euclidean space that does not adhere to the classical rules of geometry. A physicist friend told him that these odd multidimensional spaces were called orbifolds — a name chosen by the graduate students of Princeton mathematician William Thurston, who first described them in the 1970s. In the 1980s, physicists found a few applications for orbifolds in arcane areas of string theory. Now Tymoczko had discovered that music exists in a universe of orbifolds.
Tymoczko’s insight, made possible through a research collaboration with Clifton Callender from Florida State University and Ian Quinn from Yale University, has created “quite a buzz in Anglo-American music-theory circles,” says Scott Burnham, the Scheide Professor of Music History at Princeton. His work has “physicalized” music. It provides a way to convert melodies and harmonies into movements in higher dimensional spaces. It has given composers new tools to write music, has revealed new ways to teach music students, and has revealed surprising musical connections between composers as distant as Palestrina — the Italian Renaissance composer — and Paul McCartney.
In a book to be published in March by Oxford University Press, A Geometry of Music: Harmony and Counterpoint in the Extended Common Practice, Tymoczko uses the connection between music and geometry to analyze the music of the last millennium and position modern composers in a new landscape. He rejects the idea that music can be divided into distinct genres. As Tymoczko sees it, medieval polyphony, the high classical music of Beethoven and Mozart, the chromatic romanticism of Wagner and Debussy, the jazz improvisations of Bill Evans, and the Beatles’ Sgt. Pepper’s Lonely Hearts Club Band all are built on the same handful of principles. Tymoczko writes in the preface: “It would make me happy to think that these ideas will be helpful to some young musician, brimming with excitement over the world of musical possibilities, eager to understand how classical music, jazz, and rock all fit together — and raring to make some new contribution to musical culture.”
The link between geometry and music has deep roots. Sometime between 530 and 500 B.C., in the town of Kroton on the rocky southern coast of Italy, Pythagoras and his followers made one of the most consequential discoveries in the history of science. If the string of a harp is shortened by half, it creates a tone one octave above that of the unshortened string. If the original string is shortened by two-thirds, the resulting tone is separated from the octave tone by a euphonious interval we know today as a fifth. Further experimentation showed that dividing the string into four parts produces intervals now known as fourths, with fur ther divisions of the string producing the familiar 12-note chromatic scale that the Greeks bequeathed to history.
Pythagoras and his followers thought big. The rational division of the musical scale was not just beautiful or pleasing — it was a sign that the universe was constructed on a rational basis and could be understood. “It was the first consistent realization that there is a mathematical rationality in the universe and that the human mind can make sense of that rationality,” says Kitty Ferguson, the author of The Music of Pythagoras: How an Ancient Brotherhood Cracked the Code of the Universe and Lit the Path from Antiquity to Outer Space.
Two-and-a-half millennia later, fifths and fourths are still the basis not just of three-chord rock-and-roll, but of much basic music theory. Students learn how to recognize intervals and relate those intervals to different kinds of scales, like major and minor scales. They practice transposing, inverting, and modulating melodies and chords. They absorb, perhaps without fully realizing it, the mathematician Gottfried Leibniz’s injunction that music is the “unknowing exercise of our mathematical faculties.”
Tymoczko falls squarely into the mathematical tradition in music. His father, Thomas, was a well-known philosopher of mathematics at Smith College who was fascinated by the use of computers in mathematics. His sister, Julianna, is a mathematician specializing in algebraic geometry at the University of Iowa.
But Tymoczko, growing up in the 1980s in Northhampton, Mass., spent more time listening to the Talking Heads, John Coltrane, and Brian Eno than solving equations. He swapped his piano lessons for guitar lessons and began playing in bands. He entered Harvard intending to study music, but the abstract and atonal music his professors preferred left him cold, and he switched from composition to philosophy. After studying philosophy at Oxford on a Rhodes scholarship, he kicked around Harvard for a few years as a teaching assistant, composing on the side and dabbling in journalism. Finally he decided to become serious about music again and enrolled in music graduate school at the University of California, Berkeley.
Tymoczko got interested in the mathematics of music for what he calls a “selfish reason” — he wanted his music to sound better. His music is distinctly modern but also “tonal” — a term that he defines in his new book as music that adheres to several basic principles. In compositions such as “Four Dreams” and “The Agony of Modern Music” (termed “brilliant” by music critic Alex Ross), he combines the free-flowing vibe of jazz, the strangeness of 20th-century music, and the raw exuberance of the rock ‘n’ roll he listened to growing up. Combining such different kinds of music is a delicate balancing act, and to do it well, Tymoczko decided that he needed to understand music at a more fundamental level.
Early on, Tymoczko recognized that tonal music has two major distinguishing features. First, melodies tend to move short distances from note to note — a characteristic known in music theory as “efficient voice leading.” Think of the tunes you can hum off the top of your head. They probably have notes that are fairly close to each other, rather than strings of notes that jump wildly up and down. Melodies with close-together notes are easier to sing and to play on most instruments, and they’re easier to listen to.
A second important feature of tonal music is that it uses harmonies that sound good rather than bad. For reasons that aren’t entirely clear, humans (including infants) tend to prefer certain kinds of chords to other kinds of chords. Echoing the findings of Pythagoras, we tend to like chords that divide the octave almost, but not completely, evenly. Triads, seventh chords, ninths, elevenths — the archetypal chords of everything from early polyphony to jazz — divide the octave into ever-smaller but approximately equal-sized segments, much as the vertical lines on a ruler divide feet and inches into equal-sized intervals. In contrast, notes that are next to each other sound harsh and dissonant when played together, like a child banging his fists on a piano.
These two properties may seem to be unrelated. But the “amazing and mysterious” thing about music, Tymoczko says, is that each requires the other. Three singers can go from a pleasing C-major chord to the complementary and more plaintive A-minor chord by moving just one note: changing from CEG to CEA. Someone playing “Hey Jude” on the piano can move his or her fingers very little while moving from one sonorous chord to another. “Miraculously, the chords that sound good together and the ones that produce efficient voice leading are the same,” Tymoczko says.
Tymoczko and other music theorists knew that these obser vations must have a mathematical representation, and previ ous theorists had captured some of these properties using geo metric ideas. He developed an intense e-mail relationship with Quinn, Callender, and several other theorists who were working on the same general problem: How can music be captured mathematically in the most powerful possible way? “People had been coming up with ad hoc solutions,” says Yale’s Quinn. “We wanted to do something general.”
Initially, Tymoczko took an algebraic approach, representing chord progressions by equations. But a critical contribution came from Callender. In a paper published in Music Theory Online, he explained how you could arrange two-note chords on a two-dimensional surface, so that changes from one chord to another could be represented by movements of a point on the surface. However, this surface had some very odd properties. For example, if a point moving on the surface hit an edge it would essentially bounce off, like a billiard ball careening off a bumper. In mathematical terms, the surface had a discontinuity or “singularity.”
Callender, Quinn, and Tymoczko all knew that the unusual properties of the space meant that it somehow harbored additional, non-Euclidean dimensions. But how were those dimensions configured? This is where Tymoczko’s checkered academic history came in. From his time at Harvard and Berkeley, he had lots of mathematician and physicist friends. One suggested making a physical representation of the space and playing with it. That’s the piece of paper he printed out, stared at in his living room, and used to discover the Möbius strip representation of two-note chords. Tymoczko’s scientist friends also told him that when they make a big discovery they submit the work to Science. A 2006 paper by Tymoczko and a 2008 paper by all three collaborators became the first on music theory in Science’s 129-year history.
Tymoczko’s discovery of the orbifold structure of musical space immediately had an important consequence: It explained his earlier observations about efficient voice leading and euphonious chords. When orbifolds are used to represent musical sounds, the chords that most evenly divide the octave reside in the central regions of the space. For example, in the Möbius strip representation of all two-note chords, fourths and fifths occupy the central area of the strip, while dissonant chords of closely spaced notes huddle near the edge of the strip. Composers can move from one euphonious chord to another while moving short distances in the central region of a musical space. Movements of short distances correspond to notes that are close together, producing singable melodies.
The implications for composers are momentous, says Tymoczko. “Imagine that you’re a blind man in a city who knows how to get from your home and to a coffee shop. Suddenly your vision is restored. You realize that not only are the post office and coffee shop very close to each other, but that you can get there many other ways, and many of them are better than the way you knew.”
The geometric representation of music also provides a powerful way to analyze past compositions. In his new book, Tymoczko uses geometric concepts to “retell the history of Western music.” For example, on the Möbius strip representation of two-note chords, medieval composers of two-voice polyphony tended to remain near the center of the space, with occasional leaps to its edge whenever the two singers were to voice the same note. By the high classical period of Bach, Mozart, and Beethoven, composers had become experts at crafting harmonious pieces that fully exploited these central regions of musical orbifolds. Later composers then began to branch out, exploring new regions of musical space. By the 20th century, minimalist composers like Steve Reich were relying on burbling arpeggios of closely spaced notes right on the edges of orbifolds, while jazz composers like Miles Davis and Bill Evans were further exploring the chromatic spaces between the centers and edges of orbifolds pioneered by Wagner and Debussy.
This way of visualizing music provides new insights into how composers wrote some of the world’s most beautiful music. In his living room, Tymoczko plays Chopin’s “Prelude in E” through the speakers of his laptop as the computer mon itor displays a three-dimensional projection of a four-dimensional orbifold. With each new chord, a ball moves through a latticework of points on the screen. Repeatedly the prelude returns to a particular point in the lattice — representing a diminished seventh chord — from which it branches first to a chord on the immediate right and then to a chord on the immediate left. But at other points in the prelude, the ball moves freely along the lattice, a kind of improvisation more commonly associated with modern music. “Composers in the 19th century had an intuitive understanding of the bizarre geometry of musical chord space,” Tymoczko says. “In fact, they had a better feel for non-Euclidean, higher-dimensional spaces than did their mathematical contemporaries.”
Tymoczko’s approach also makes it possible to compare very different kinds of music. At various times in his new book he compares Schumann’s “Chopin” movement in Carna val to Nirvana’s “Heart-Shaped Box,” Shostakovich’s “G-Minor Piano Quintet” to the Black Sabbath song “Sabbath, Bloody Sabbath,” and Philip Glass’ opera Einstein on the Beach to the opening of the TV show Battlestar Galactica. “Music that superficially seems quite different, like Renaissance music and jazz, make remarkably similar use of musical space,” he says.
In fact, Tymoczko argues, the music of the past millennium in the West, and much of non-Western music as well, constitutes an “extended common practice” characterized by the continued broadening of usable musical space. That history has, of course, been shaped by the creativity and idiosyncrasies of individual composers. But it has followed certain broad paths because of how musical orbifolds are configured. It’s like a mountaineer ascending a rock face, he says. In principle, the climber is free to move in any direction. But the structure of the rock provides certain natural routes, offering handholds and footholds along the way. “The trick for the historian is to make room for historical contingency while also capturing the way in which music history sometimes follows the path of least resistance, like a climber ascending a cliff by way of a particularly inviting chute.”
Tymoczko’s work falls into the category of basic research — it doesn’t have a guaranteed payoff. Yet already it’s finding lots of applications. Among the first enthusiasts were composers who use computers to produce musical ideas — and in some cases, complete compositions. Composer Michael Gogins, for example, uses orbifolds to add harmonic and melodic structure to notes generated randomly by the computer. “It gives you more power,” he says.
Some music theorists have begun using orbifolds to teach composition and theory to undergraduates, a trend Tymoczko hopes his new book will encourage. The value of the idea, says Quinn at Yale, is that a geometric approach demonstrates both the possibilities and constraints of music. “Once composers said, ‘Let’s get out of the box,’ that’s when they began wrapping themselves around the singularities and other weird parts of the space.”
Other applications of orbifolds are still on drawing boards. Tymoczko envisions orbifold-inspired children’s toys that could teach chord structure through play. A dancer could move through a space wired to generate the chords associated with each location. Composers could write music by moving through orbifolds rather than writing notes on staves.
Has the discovery of music’s geometry achieved Tymoczko’s original purpose — to make his music sound better? It helps, he says, but it can’t replace inspiration. Composition has both a mechanical phase and a mysterious phase. The use of geometric ideas can suggest melodies and harmonies — it frees a composer “from repeating the formulas of the past.” But when he’s writing music, says Tymoczko, who is working on an album of jazz, funk, and classical fusion pieces, the mechanical part must be followed by the mysterious part, when a composer “learns what a piece is really about.”
The saxophone genius Charlie Parker put it a bit differently: Learn all the theory you can, he said, and then forget it when you play.
Steve Olson, based in Seattle, has written about genetics, race, evolution, climate change, talent, and punk-rock music, among other things. His most recent book, Anarchy Evolution: Faith, Science, and Bad Religion in a World Without God, co-written by Greg Graffin, was published in September by itbooks.


