With apologies to William Blake, who once urged us to “see a world in a grain of sand,” the speck that Paul Steinhardt is holding — glued to the point of a glass needle because you’d never find it again if it weren’t — is barely visible to the naked eye. Steinhardt’s enthusiasm notwithstanding, a visitor to his fourth-floor office in Jadwin Hall is only being polite when he acknowledges that he can see it at all.
But Steinhardt is a theoretical physicist, so let your mind bore in to the atomic level. This speck is called a quasicrystal, a rare 20-sided clump of atoms that violates what were long believed to be the most basic rules of crystalline structure. Three decades ago, an Israeli physicist, Daniel Shechtman, stumbled upon man-made quasicrystals in a piece of industrial aluminum and later received the Nobel Prize for his discovery. But Steinhardt already had deduced that such structures might exist, and it was he and his co-author who explained what Shechtman had found.
Having looked within, now pull back. Rewind the probable history of this speck like one of those reverse-action films in which the diver emerges feetfirst from a pool and arcs up onto the board. Follow it back to the piece of khatyrkite, the rare mineral in which it once was embedded; back into the white cardboard box in the collection of the University of Florence; back into the black-market collection of an Amsterdam gem dealer. Go further, to the remote Russian stream bed where a platinum prospector first picked up the khatyrkite 32 years ago, to the glacier that dropped it during the last Ice Age 15,000 years ago, to the meteorite that disintegrated in the atmosphere and rained stardust over Siberia.
Don’t stop. Reassemble that meteorite and pull it back into the sky, out of our galaxy, out into the farthest reaches of space, where Steinhardt thinks it may have formed in a collision with another meteorite. Chemical analysis suggests that this little bit of metal ricocheted around the universe for 4.5 billion years. It is older than our solar system yet something never seen before, and it could fit on the head of a pin.
How about that, William Blake?
Officially, Steinhardt is the Albert Einstein Professor in Science (and director of the Princeton Center for Theoretical Science), but his three-decade investigation of quasicrystals has required him to be part Carl Sagan, part Indiana Jones, part Lewis and Clark, and part Sherlock Holmes. Throw in a touch of Captain Ahab, as well, for it is not too much to say that in the world of crystallography those rare specks of metal have become — if one can lurch to the opposite end of the metaphorical scale — the Great White Whale.
Face to face, Steinhardt is mild-mannered and engaging, with an uncommon ability to explain opaque scientific concepts in layman’s terms. That is helpful, for his interests range among particle physics, dark energy, astrophysics, and cosmology. One of the founders of an inflationary model of the universe, which holds that the early universe underwent a period of exponentially rapid expansion, he since has developed a competing theory, a so-called cyclic model, which posits that the universe oscillates through periods of expansion and contraction. (See “The Cosmic Apocalypse,” PAW, Feb. 11, 2009.) A prolific writer and lecturer, Steinhardt has co-authored one book and edited four more, published more than 200 journal articles, and received six patents relating to quasicrystals, with two more pending.
The best way to understand quasicrystals is to look at something two-dimensional. Think of your bathroom floor. Chances are, the tiles are laid in a regular, repeating pattern. If the pattern is made with a single type of tile, only certain shapes — three-, four-, or six-sided — can be used to fill the space completely. Use pentagons, octagons, or any other shape, it was believed, and there will be space left over.
Physicists long thought that the atoms inside a crystal also arranged themselves in repeating patterns. Like those floor tiles, only certain shapes were permissible, and only certain types of symmetries — two-, three-, four-, or sixfold — were possible (in other words, each piece or atom could be rotated a certain number of degrees and still fit in the pattern). Starting in the 1960s, mathematicians tried to see if it were possible to arrange tiles in a pattern that never repeated itself — that was, to use the scientific term, nonperiodic. A British mathematician, Roger Penrose, created such a pattern using two shapes, a fat and a thin rhombus.
In the early 1980s, Steinhardt began working with a graduate student, Dov Levine (now a theoretical physicist in Israel), when both were at the University of Pennsylvania, to see if they could find atomic arrangements with supposedly impossible symmetries. Looking at Penrose’s two-dimensional mosaic, they discovered that the pattern thought to be nonperiodic was actually quasiperiodic, meaning that the pieces did follow a pattern, although that pattern never perfectly repeated itself.
At the same time, Shechtman, working at what is now the National Institute of Standards and Technology, accidentally discovered an aluminum alloy that, when viewed under an electron microscope, was seen to contain crystals with fivefold symmetry. Not only did no one believe him — crystals couldn’t have fivefold symmetry — his supervisor reassigned him and suggested that he learn something about crystallography. It took two years before any scientific journal would agree to publish Shechtman’s findings.

While Shechtman’s article was out for peer review, a mutual friend brought a copy to Steinhardt. As soon as he saw the unique X-ray diffraction pattern for Shechtman’s aluminum sample, Steinhardt rushed to his desk and pulled out a copy of a quasiperiodic pattern he and Levine had predicted. They matched exactly. Shechtman had not understood how the atoms in such an alloy could be arranged to produce the odd symmetry he had seen, but Steinhardt did. In December 1984, five weeks after Shechtman’s article appeared, Steinhardt and Levine published their own article in which they dubbed these structures quasicrystals. (Steinhardt and Peter Lu ’00, now a postdoctoral research fellow at Harvard, since have discovered that medieval Islamic artisans had designed quasiperiodic wall mosaics 700 years before the concepts behind them were understood in the West. Their findings, published in the journal Science in 2007, made the front page of The New York Times.)
In the decades since Shechtman’s discovery, more than 100 types of quasicrystals have been produced for industrial uses. Because quasicrystals are poor conductors of electricity, they are good insulators; and because they are unusually hard and slippery, they have been put into ball bearings, razor blades, and nonstick coatings. All have been created in the laboratory under tightly controlled conditions.
Steinhardt, however, wondered if quasicrystals also might occur in nature. Off and on for more than a decade, he searched through mineral collections in major museums — until shortly after he arrived in Princeton in 1997, when geosciences professor Kenneth Deffeyes *59 introduced him to Lu. Then a junior, Lu was something of a geological prodigy who had won the national gold medal for mineral collecting four times while in high school. Lu and Steinhardt devised an algorithm to hunt for quasicrystals through their unique X-ray diffraction patterns.
Fortunately, there is an international database of such diffraction patterns for 80,000 different natural and manmade materials. After plowing through them, Steinhardt and Lu identified six minerals that looked promising, tracked down samples, and had each analyzed at the Princeton Institute for the Science and Technology of Materials (PRISM). By 2001, after four years of work, they had found ... nothing. Steinhardt and Lu published a paper announcing their failure and asked for help from anyone who might have access to rare minerals.
Six years later, in 2007, Luca Bindi, director of the mineral collection in the natural history museum at the University of Florence in Italy, told Steinhardt there might be a promising candidate in a collection of 10,000 mineral samples his museum had acquired back in 1990. He spent more than a year checking likely candidates without success. Finally, in late 2008, Bindi suggested that Steinhardt test a sample of a rare rock called khatyrkite. Bindi prepared a sample and sent it to Princeton for X-ray diffraction. On New Year’s Day in 2009, Steinhardt rose at 5 a.m. and went in to the lab to watch PRISM imaging and analysis director Nan Yao test this tiny piece of khatyrkite.
“We popped it into the machine,” Steinhardt recalls, “and wow! This was much better than Shechtman’s pattern. I never thought I would see anything in nature that was that good. There was no question that what we had there was a quasicrystal.”
There were questions, however. This quasicrystal, an aluminum-copper-iron alloy (Al63Cu24Fe13), appeared as a granule in a rock about 3 millimeters wide that was studded with a number of other extremely exotic minerals, like chocolate chips in a cookie. One of those chips was a piece of nearly pure metallic aluminum. Geologists were convinced that metallic aluminum does not exist naturally on earth; the metal reacts so strongly with oxygen that it is always found as aluminum oxide. The oxygen has to be processed out to produce the aluminum used in foil, siding, and other familiar products.
On New Year’s afternoon, Steinhardt sent his colleagues an email wishing them a “Happy Quasicrystal Day.” Deffeyes, however, refused to believe that Steinhardt had found what he thought he had found. “I want no part of this one,” he said, but he did refer Steinhardt to his colleague Lincoln Hollister, who began his career studying rocks from the Apollo moon expeditions. Hollister, too, told Steinhardt that this quasicrystal must have come from some industrial plant, but he agreed to try to help solve the mystery.
Hollister took Steinhardt to Washington, D.C., to meet a former graduate student, Glenn MacPherson *81, who was working for the Smithsonian as a meteor geologist. MacPherson delivered the same verdict. “I’m sorry,” he said, “but what you have there is impossible.”
As Steinhardt kept badgering, Hollister and MacPherson conceded that such a crystal might — theoretically — have formed naturally under intense heat and pressure. But there were only two places where such conditions might exist. One was deep inside the earth, near the boundary between the core and mantel, and the other was deep in outer space. Steinhardt took this as a victory. “So it’s not impossible, it’s just really unlikely,” he recalls thinking. “That means you try harder, you don’t give up.”
The only way to prove that this sample was natural and not man-made was to examine more of it. Unfortunately, Bindi had been forced to destroy the only piece available in preparing it for the X-ray diffraction.
They would have to find more khatyrkite.
Where had Bindi’s museum gotten its sample? The only clue the scientists had to go on was the box it arrived in, which said that it had been found in a remote part of eastern Russia and been bought from an Amsterdam gem dealer named Nicholas Koekoek. Steinhardt and Bindi tried to trace Koekoek, but the trail was cold. Scouring the Internet, they found four more museums that claimed to have khatyrkite, but three of the samples turned out to be fakes. The fourth, in a museum in St. Petersburg, Russia, was the world’s holotype of khatyrkite — the physical example used when the specimen first was formally described — and thus could not be dissected.
Steinhardt tracked down the Russian scientist who had announced the discovery of khatyrkite in 1985, a man named Leonid who once headed the Soviet Union’s platinum institute. He refused to help. A few months later Bindi was in Florence and mentioned his fruitless search for Koekoek the gem dealer to a dinner companion, who was from Amsterdam. The friend remarked that a neighbor had the same surname. The woman turned out to be Koekoek’s widow.
Bindi traveled to Amsterdam to meet with the widow, who showed him a diary in which her late husband had recorded his transactions. In it, Koekoek mentioned that he had gotten khatyrkite in Romania from a man identified only as “Tim.” That was hardly enough to go on, but then the woman produced a second, secret diary. This one stated that Tim the Romanian actually was Leonid. The Russian scientist, it seemed, had been selling rare minerals on the side while working at the Soviet platinum institute.
Steinhardt and Bindi then reread the Soviet scientist’s paper, which reported that the sample had been found in the Listvenitovyi stream in the Koryak mountains by a man named Valery Kryachko. Finally the scientists chanced upon a 1990 paper that listed Valery Kryachko as a co-author. Steinhardt located the lead author of this paper in Moscow, and he put Steinhardt and Kryachko in touch.
Kryachko proved to be all that Steinhardt hoped he would be. In 1979, Kryachko told Steinhardt, he was sent to northeastern Russia to look for platinum. After spending several days along an old gold-mining stream (platinum often is found near gold veins), he had nothing to show for his efforts, and picked up several pieces of an interesting-looking mineral to prove that he had been out in the field. He still had his maps and was sure he could find the spot again.

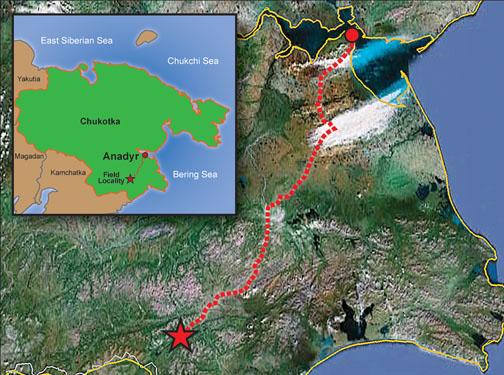
Over the next year and a half, Steinhardt raised money for a field expedition from a private donor (Steinhardt won’t say how much or from whom) and assembled a team of 10 scientists including MacPherson, Cornell geologist Chris Andronicos *99, and Mike Eddy ’11, now a graduate student at MIT, as well as two drivers and a cook. In July 2011, they set off.
The Koryak region is in far northeastern Russia, just across the Bering Sea from Alaska. It is accessible for only about three weeks a year; the rest of the time it is buried under snow or boggy permafrost. Planes took the group as far as the mining town of Anadyr, about 217 miles from their destination, but even traveling in trucks equipped with tank treads, it took them four days, crawling at about 10 miles an hour, to reach the area. They had to hike the last few miles on foot.
Once the researchers reached the right stream, they spent 10 days fighting clouds of mosquitoes and watching for bears. The stream bed’s blue-green clay was so thick, Eddy says, that it snapped their shovels in half, forcing them to scoop out small clumps by hand. Temperatures in the rushing water were barely above freezing, even in mid-summer; diggers had to warm their hands first over a fire before plunging them into the stream. Their one luxury came at mealtimes; the salmon were running, and the Russians would squeeze fresh caviar out of them before grilling the meat, washing it all down with an ample supply of vodka.
Detecting a quasicrystal in a ton and a half of clay was like looking for a needle in a very mucky haystack. It fell to Kryachko, an experienced gold-miner, to pan through the mud and sift out promising nuggets, which MacPherson then examined under a field microscope. Other members of the team, meanwhile, surveyed the area and looked (unsuccessfully) for a possible meteor-impact crater.
It was not until a month after their return that laboratory analyses confirmed that they had found more natural quasicrystals — nine in all, each the size of a grain of sand. Steinhardt, Bindi, Yao, and Lu have named the material icosahedrite, because the molecules that comprise it have an icosahedral (20-sided) shape, like the panels of a traditional soccer ball.
Compared to the rest of the project, the effort to determine where this khatyrkite formed was relatively easy. Materials originating on Earth contain very different ratios of oxygen isotopes than those originating in outer space, Steinhardt explains, and the ratio of oxygen isotopes in khatyrkite is consistent with a rare kind of meteorite called carbonaceous chondrite, which formed at the beginning of the universe. The khatyrkite also contained pieces of another mineral, stishovite, that often is found in meteorites. Although several scientists questioned Steinhardt’s first reports that he had found a natural quasicrystal in a meteorite, these isotope studies have put those doubts to rest.
The discovery of a natural quasicrystal is significant, says Deffeyes, who is retired and living in California. “These types of quasicrystals were thought to be a lab curiosity. To find one in nature says that this thing has stood around for billions of years without altering into something else. That means it’s stable. I didn’t think they had the chance of a snowball in hell, but now I’m a believer rather than a skeptic.”
Naturally occuring quasicrystals also may force scientists to rethink geology. Finding a natural quasicrystal, Bindi writes in an email from Italy, “dramatically changes the history of this discipline, expanding the catalog of materials formed by nature. The definition of a mineral (reported in all the textbooks of mineralogy) as material characterized by an ordered and periodic structure would have to be modified, forever.”
A.J. Stewart Smith *66, the Class of 1909 Professor of Physics and dean for research, agrees. “This changes people’s views of crystallography and what structures are possible,” he says. “That’s fundamental.”
In science, however, each answer only raises new questions. Steinhardt and Hollister now are trying to determine exactly how this quasicrystal formed and what that might tell us about the formation of the galaxies. Steinhardt also has been talking to scientists who are interested in sending a probe to an orbiting asteroid, where conditions might have produced other quasicrystals.
Robert Downs, a scientist at the University of Arizona, speculated in Science News that these crystals might have been born in the shock waves from a supernova that formed the sun and the planets. This discovery, he predicted, “will tell us something fundamental about the process that created the material that formed our solar system.”
So another journey begins — and who knows how long this one will take? Steinhardt is enthusiastic. “When I work on a problem, I let the problem lead me to the next thing,” he explains. “One thing I’ve learned on this project is, you just have to go all in. Never let anything go. And that continues to this day.”
Mark F. Bernstein ’83 is PAW’s senior writer.



